перейти на главную страницу                                               перейти на список публикаций

УДК 678.021.16

Я.Г. Двойнос, аспирант

(Национальный технический университет Украины, “Киевский политехнический институт”, Киев)

            Моделирование переработки волоконно- наполненных полимерных композиций методом червячной экструзии.

            Решена задача моделирования процессов, связанных с переработкой расплавов высоконаполненных полимерных композиций методом червячной экструзии. Предложена методика расчета оборудования.

            Розв’язана задача моделювання процесів, пов’язаних з переробкой розплавів високонаповнених полімерних композицій методом черв’ячної екструзії. Запропанована метода розрахунку устаткування.

            Ключевые слова: высоконаполненные композиции, моделирование, полимер, червячный экструдер.

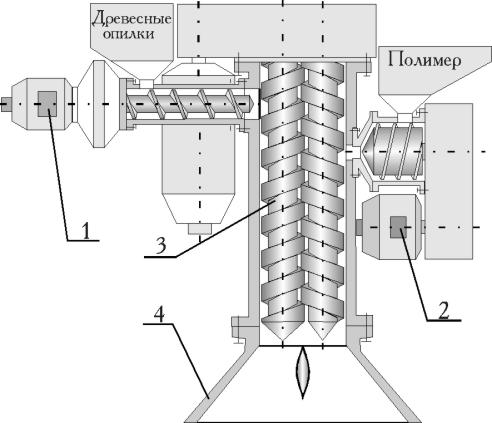
            Постановка задачи. Современные технологические схемы получения изделий из композиционных полимерных материалов на базе червячной экструзии предполагают совмещение материала наполнителя с расплавом полимера в отдельном смесительном двухчервячном экструдере [1]. АО “Большевик” г.Киев, совместно с кафедрой Машин и аппаратов химических и нефтеперерабатывающих производств “КПИ” разработано и внедрено оборудование для производства листов и погонажных изделий из древесно-наполненных полимеров, схема приведена на рис.1а. Основные затраты на производство линии связаны с изготовлением смесительного двухчервячного экструдера, его замена на одночервячный экструдер при сохранении качества смешения позволяют повысить конкурентные возможности всей линии путем снижения ее себестоимости и увеличения срока службы.

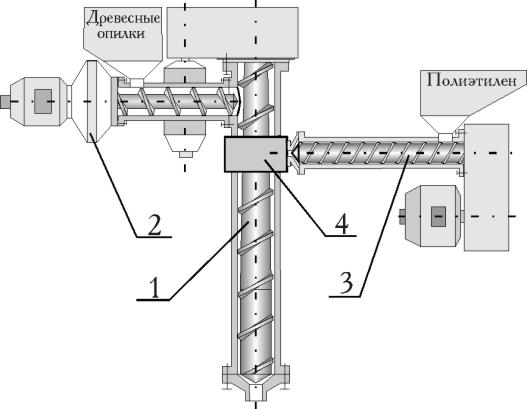
Эта модернизация стала возможной после проведения необходимых научных и экспериментальных работ [2]. В настоящее время выполнена полная конструкторская документация на новую линию, рис.1б. Патентуются новые конструкторские решения.

            Математическая модель процесса течения расплава высоконаполненного полимера в канале червяка одночервячного экструдера. Можно выделить следующие особенности моделирования течения композиционного материала в канале червяка.

1. Расплавы композиций обладают выраженными аномалиями вязкости, проявляется эффект проскальзывания на стенках [4].  2. После попадания наполнителя в расплав образуются агломераты несмоченного наполнителя, увеличение гидростатического давления ведет к росту механической прочности этих агломератов. Моделирование процесса диспергирования представлено в работе [5], исходными данными являются поля сдвиговых напряжений.                      

3. В канале червяка образуются зоны с разной концентрацией наполнителя и, как следствие, с разными реологическими параметрами.

            Учитывая эти особенности, для моделирования использовался подход, предложенный в [6].

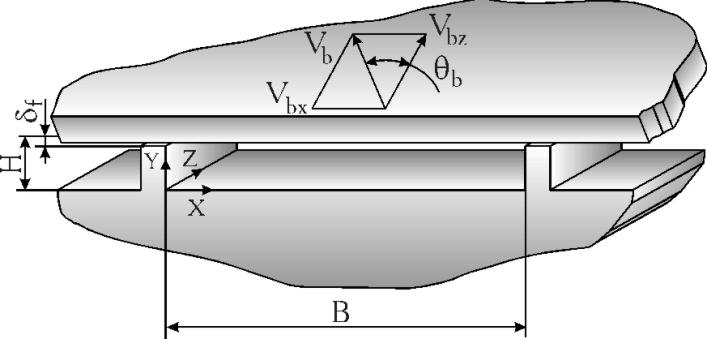
Для анализа рассмотрим плоскопараллельную модель канала червяка  [3а], рис.2.

Уравнения движения записываются:

в работе [3б, 7а] получены следующие уравнения, описывающие изменение напряжений по оси Y:

где  и  - сдвиговые напряжения у основания червяка. Граничные условия:

            Уравнения неразрывности в интегральной форме [3с]:

Учитывая граничные условия (4) получаем:

            Для описания поведения расплава композиции волоконно-наполненного полимера используем группу уравнений обобщенной неньютоновской жидкости:

Используя предложенную в [6] форму реологической зависимости:

где f - функция, выражающая связь между инвариантом тензора напряжений и эффективной вязкостью. Используется второй инвариант тензора напряжений, который при принятых допущениях имеет вид:

Учитывая (11) и (12), уравнения (9-10) запишутся:

С учетом (1-2) получаем:

Полученные зависимости позволяют определять скорость сдвига в точке с заданными температурой и концентрацией наполнителя. Поскольку последние являются переменными величинами, то общий вид реологической функции будет иметь вид:

При принятии допущения о зависимости температуры и концентрации наполнителя в выбранном поперечном сечении канала только от глубины канала: T¹f(x), C¹f(x), и зная эти зависимости:

можно перейти к более простой форме записи:

Для моделирования течения с проскальзыванием на стенках необходимо реологическую зависимость дополнить условиями скольжения на стенках (y=0,H) [4]:

где  - коэффициент трения скольжения. Как будет показано далее, эта зависимость понадобится на последнем этапе расчетов. Используя (4, 5, 6, 7, 8, 13, 14, 15) запишем систему уравнений:

Независимыми переменными являются: . Целевая функция запишется:

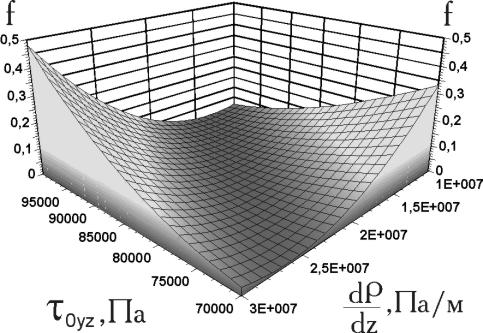
Решение математической модели: Для правильного выбора метода оптимизации целевой функции предварительно исследовалась одномерная модель течения и использовался метод сканирования. На рис. 3 показана зависимость целевой функции от двух независимых параметров () для лабораторного экструдера

 (D=0.09m, H=5mm, N=25мин^-1, Q=55kg/h) и древесно-полиэтиленовой композиции с наполнением 47% по массе (T=473’K, K=18500, n=0.64 -модель степенной жидкости) при допущении однородности температурного и концентрационного полей.

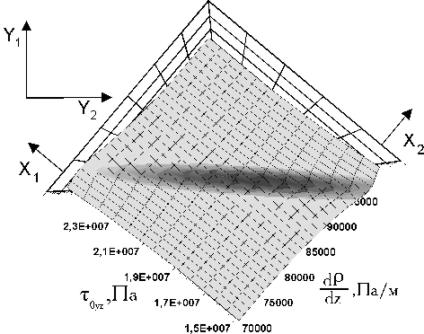
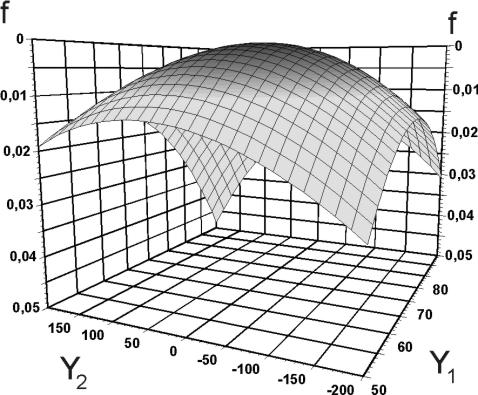
            Монотонность функции, отсутствие “оврагов” и единственность решения были установлены и при других параметрах. Для дальнейшего анализа была введена дополнительная система координат (Y1,Y2), повернутая относительно начальной на угол 55⁰ по часовой стрелке.

Более детальное исследование близлежащей к оптимуму области подтвердило предположение о монотонности функции и единственности решения, рис. 4. Окончательно для оптимизации двухмерной модели были выбраны метод Гаусса-Зейделя и метод поворота осей с последующим методом наискорейшего спуска.

          Разработанные алгоритмы и программы расчета были проверены численно по отношению к моделям течения в канале червяка ньютоновской жидкости Тадмора [3а] и модели течения степенной жидкости Торнера [7б]. Для ньютоновской модели жидкости получена полная сходимость результатов, для степенной модели сходимость результатов зависит от степени неньютоновского поведения жидкости и обусловлена погрешностями базовой модели.

Анализ результатов: На базе предложенных алгоритмов решения математической модели предлагается новая методика расчета проектируемого оборудования. Входными параметрами для расчета являются геометрия канала, скорость вращения червяка (варьируемые параметры), реологические свойства среды, обьемный расход и температура расплава на входе в экструдер. Результатом расчетов является значение градиента давления вдоль канала, поля скоростей и напряжений. Последние позволяют определять среднеинтегральное на витке повышение температуры расплава и напряжения на границах канала. По известным сдвиговым напряжениям на границах определяется мощность привода и возможность проскальзывания расплава на стенках. Как показали эксперименты, проскальзывание на стенках экструдера недопустимо, поскольку приводит к пульсациям производительности, локальным перегревам материала и пробковому движению композиции без смешения. Исходя из этого расчет направлен на поиск такой геометрии червяка и скорости его вращения, при которых обеспечивается максимальная производительность, отсутствует скольжение на стенках и развиваемое давление достаточно для преодоления сопротивления диспергирующих насадок. Кроме этого контролируется рост температуры и оценивается диспергирующая способность по известным полям сдвиговых напряжений и значениям гидростатического давления.

Литература

1. Миани М. Машины и оборудование для производства полимерных листов и пластин из полиолефинов с древесной мукой. Вестник внешторга Италии. - 1993.-№5.-с.1-18.

2. Исследование процесса переработки композиционных полимер содержащих материалов и разработка технологии получения из них листов. Отчет о НИР/Киевский политехн. ин-т.- Инв. №5232/07.-К.,1993.-с.6-38.

3. Тадмор З., Гогос К. Теоретические основы переработки полимеров. пер. под ред. Торнера Р.В.- М.: Химия, 1984.- а)с. 319-322, б)с. 307.

4. Гладышев В.И., Чепура И.В., Генералов М.Б. Методика расчета расходно-напорных характеристик роторного пресса с учетом пристенного скольжения скольжения на неподвижной стенке.// Химическое и нефтяное машиностроение. 1995. №8. С. 1-4.

5. Ким В.С. Исследование смешивающей способности экструзионных машин и разработка основ теории и методов расчета процессов смешения полимерных материалов в экструдерах. Автореф. дис. ...докт. техн. наук. М.: МИХМ, 1979. 32с

6. Воскресенский А.М., Войцеховский В.Б., Коугия Ф.А. Моделирование переработки в одночервячных машинах полимеров с произвольной аномалией вязкости. //Химическое и нефтяное машиностроение. 1995. №1. С. 13-17.

7. Торнер Р.В. Теоретические основы переработки полимеров. - М., Химия, 1977,- а)с.247, б)с.118-128.

            ДВОЙНОС Ярослав Григорьевич, аспирант, м.н.с. кафедры машин и аппаратов химических и нефтеперерабатывающих производств Национального технического университета Украины “Киевский политехнический институт”. В 1993 году окончил Киевский политехнический институт. Область исследований - переработка полимерных композиций методами червячной экструзии.

   перейти на главную страницу                                               перейти на список публикаций