
перейти на главную страницу перейти на список публикаций
Моделирование процессов смешения при переработке пластических масс в одночервячном экструдере.
Процессы смешения имеют важное значение при переработке полимерных материалов в изделия и детали, так как качество смешения определяет качество изделия. Появившееся в последнее время большое количество изделий, изготовленных из наполненных полимеров, обусловило интерес к моделированию процессов смешения [1-4]. Во многих случаях качество смешения оценивается по таким параметрам, как накопленная деформация, время пребывания, напряжения сдвига при диспергирующем смешении и др. Как правило, эти показатели являются интегральными и не всегда дают возможность получить полное представление о процессе смешения.
Предложен и реализован новый подход к моделированию процесса смешения наполненных полимеров, основанный на использовании компьютерной техники.Сущность метода состоит в моделировании процесса смешения путем пересчета координат моделирующих точек, находящихся в определенном поле скоростей. Условием реализации подхода является определение скоростных полей расплава в рабочих органах оборудования. Для ламинарного смешения эти поля определены в литературе для многих случаев течения, например для некоторых каналов простой формы в табл. 1 [3].
Начальное распределение частичек наполнителя в канале червяка моделируется таким же начальным распределением точек, координаты которых вводятся в компьютер. Принимая во внимание достаточно сложные зависимости для определения скоростей этих частичек, для ускорения счета в разработанной программе вначале определяются значения локальных скоростей в узловых точках рабочих полостей оборудования и запоминаются в виде таблиц.
С помощью таких таблиц методом интерполяции можно определять значения локальных скоростей в любых точках, что значительно ускоряет вычисления. Интерполирование осуществляется сплайнами с заданной сеткой узлов [7]. Узловые точки располагаются таким образом, чтобы они ложились на границах и внутри канала. В качестве примера на рис. 1 показана двумерная сетка узлов канала червяка одночервячного экструдера, имеющая 81 узел.
Таблица 1.
Профиль скоростей ньютоновской жидкости через каналы простой формы
|
Течение между параллельными пластинами |
Вынужденное течение |
Vz=x*V0 |
|
Течение под давдением |
Vz=4*x*(1-x)*Vmax |
|
|
Течение при наложении давления на вынужденный поток |
Vz=[x+3*x*qp/qd*(1- x)]*V0 |
|
|
Течение через круглую трубу |
|
Vz=(1-r^2/R^2)* Vmax |

Рис.1
Для проверки правильности задания поля скоростей и алгоритма интерполяции, достаточности узловых точек (профиль скорости должен быть плавным, а не ломаным), условий неразрывности ( моделирующие точки не должны выходить за пределы канала), принятия расчетной единицы времени, для которой пересчитываются новые координаты моделирующих точек, разработана тестирующая программа. Фрагменты вычислений по этой программе для канала червяка и ньютоновского профиля скорости приведены на рис. 2 и 3.

рис. 2
В верхней части рисунка в принятом масштабе изображен развернутый канал червяка в продольном сечении. В нижней части рисунка изображен канал червяка в поперечном сечении. Кривые изображают скопления моделирующих точек. Начальное распределение моделирующих точек в режиме тестирования программы задается на прямой, это позволяет определить ошибку в задании поля скоростей и определить необходимое количество узлов интерполяции. На рис. 3 показан фрагмент тестирующей программы, количество узлов принято равным 9 (для сравнения, на рис. 2 - 81 узел интерполяции), явно видена ломаная структура поля скоростей, полученных интерполяцией.
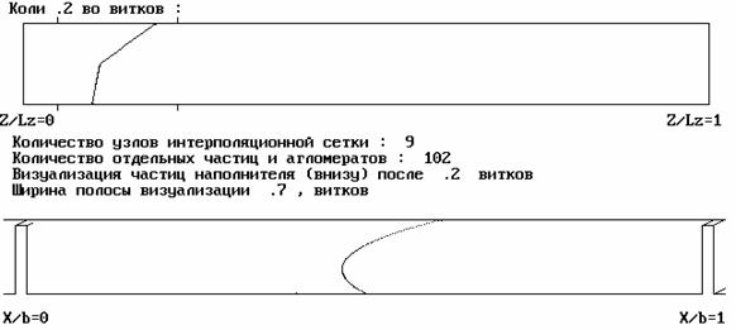
рис. 3
В случае двумерного описания поля скоростей необходимо введение некоторых формальных условий. Так, например, при использовании плоскопаралллельной модели червяка и принятии предпосылки Vy=0 может быть использовано следующее условие. При приближении моделирующей точки к стенке канала она переносится в другую точку относительно координаты с нулевым значением поперечной скорости и новая ее координата, рис. 4 (при принятии модели Бернхарда) определится из уравнения:
Ynn=Ywo-(Ywo/(H-Ywo))*(Yn-Ywo) (1)
|
|
Здесь Yn - начальная координата Y моделирующей точки, Ywo - координата Y с нулевой поперечной составляющей скорости моделирующего потока, H - высота канала червяка, Ynn - новая
|
рис. 4 (расчетная) координата Y мо-
делирующей точки. Поперечная составляющая скорости для ньютоновской модели определяется при этом по уравнению:
Vx=Ux*[3*(Y/H)^2-2*(Y/H)] (2)
(6), где Ux - поперечная составляющая скорости стенки цилиндра, H- высота канала, Y- текущая координата высоты. Приняв Vx=0 получим Ywo=H*2/3.
В работе [8] изучается расположение линий тока в циркуляционном течении расплава полимера в поперечном сечении канала червяка для случая неньютоновского течения. Если пренебречь наличием утечек, то расход через верхнюю область равен расходу через нижнюю область и координаты линий тока в верхней и нижней областях оказываются связанными следующим интегральным соотношением:
(3)
где - текущее значение координаты высоты в безразмерном выражении: Y/H (4)
где Y - абсолютная координата высоты, м;
H - высота канала червяка, м;
Для оценки влияния неньютоновского течения на положение линий тока в поперечном сечении канала червяка приведем данные:
при изменении индекса течения n в диапазоне 1< n < 8, координата нулевой поперечной составляющей скорости в безразмерном выражении (4) изменяется в пределах 0.66 < < 0.85 [9], это учитывается в разработанном алгоритме.
Алгоритм расчета процесса смешения приведен на рис. 5. Визуализация на дисплее моделирующих точек в поперечном сечении канала (нижняя часть рисунков) осуществляется после попадания их в зону Z, находящуюся на определенной координате Z. В качестве примера на рис. 6 показано начальное распределение моделирующих точек. На рис. 7 представлена картина процесса смешения после 5 секунд от начала ввода наполнителя, в нижней части рисунка видны только точки, попавшие в область, расположенную на расстоянии 2 витков от зоны ввода наполнителя и имеющую ширину 0.5 витка. Важно отметить, что поскольку в реальном процессе загрузки частиц наполнителя они распределяются случайным образом в определенной зоне канала червяка, то и при задании начального распределения моделирующих точек необходимо задавать их координаты случайным образом (при этом они должны попадать в определенную зону канала червяка). Это требование обьясняется еще и тем, что если задавать начальное распределение моделирующих точек одинаковым, то траектории моделирующих частичек будут одинаковыми (для загрузки наполнителя в разные моменты времени).
Очевидно,
что чем уже зона визуализации Z, тем точнее картина процесса, однако это
требует увеличения числа моделирующих точек, что ведет к увеличению затрат
машинного времени для расчетов. С целью ускорения расчетов и снижения требований
к размеру памяти компьютера предложен способ, заключающийся в том, что
визуализируются не только моделирующие частички, находящиеся в этот момент в
зоне визуализации, но и положения всех моделирующих точек, когда они проходили
интересующую нас область. Естественно, Z можно сделать минимальной (она
принимается расстоянию, которое преодолевает самая быстрая частица за расчетную
единицу времени).
|
|
|
рис. 5 |

рис. 6
Таким образом, разработанная программа моделирует процесс смешения в каналах экструдера, дает возможность визуализировать процесс смешения и оценить однородность композиции на всех участках зоны смешения визуально, что является одним из важнейших методов оценки качества смешения на практике, особенно это важно, когда необходимо гарантировать отсутствие текстуры на изделии, или наоборот, выполнить изделие с определенной текстурой. Кроме этого, программа позволяет вычислить все показатели оценки качества смешения. Ее можно применить для расчета смешения в каналах сложной формы комбинированных экструдеров, если сформулировать условия стыковки скоростных полей. Есть возможность учета неравномерной работы дозирующего оборудования.
Литература
1. Ким В.С. Исследование смешивающей способности экструзионных машин и разработка основ теории и методов расчета процессов смешения полимерных материалов в экструдерах. Автореф. дис. ...докт. техн. наук. М.: МИХМ, 1979. 32 с.
2. Ким В.С., Скачков В.В. Диспергирование и смешение в процессах производства и переработки пластмасс.- М.: Химия, 1988.- 240 с.
3. Тадмор З., Гогос К. Теоретические основы переработки полиме-ров//пер. с англ. под ред. Торнера Р.В., М., Химия, 1984.
4. Калинская Т.В., Доброневская С.Г., Аврутина Э.А. Окрашивание полимерных материалов.- Л.: Химия, 1985., ил. 5. Мак-Келви Д.М. Переработка полимеров.//пер. с англ., Химия,М., 1965.
6. Бернхардт Э. Переработка полимеров.- М.: Химия, 1965.-442с.
7. Овчинников П.Ф., Лисицын Б.М., Михайленко В.М. Высшая математика. Под ред. Овчинникова П.Ф., Киев, Высшая школа, 1989. 8. Giegerich V., “Plastverarbeiter”, 1974, Bd. 25, №3, S. 145-150.
9. Торнер Р.В. Теоретические основы переработки полимеров.- М,: Химия, 1977.
перейти на главную страницу перейти на список публикаций